2025. 3. 20. 19:31ㆍ프로그래머스/LV.3
문제링크: 섬 연결하기
문제설명
n개의 섬 사이에 다리를 건설하는 비용(costs)이 주어질 때, 최소의 비용으로 모든 섬이 서로 통행 가능하도록 만들 때 필요한 최소 비용을 return 하도록 solution을 완성하세요.
다리를 여러 번 건너더라도, 도달할 수만 있으면 통행 가능하다고 봅니다. 예를 들어 A 섬과 B 섬 사이에 다리가 있고, B 섬과 C 섬 사이에 다리가 있으면 A 섬과 C 섬은 서로 통행 가능합니다.
제한조건
- 섬의 개수 n은 1 이상 100 이하입니다.
- costs의 길이는 ((n-1) * n) / 2이하입니다.
- 임의의 i에 대해, costs[i][0] 와 costs[i] [1]에는 다리가 연결되는 두 섬의 번호가 들어있고, costs[i] [2]에는 이 두 섬을 연결하는 다리를 건설할 때 드는 비용입니다.
- 같은 연결은 두 번 주어지지 않습니다. 또한 순서가 바뀌더라도 같은 연결로 봅니다. 즉 0과 1 사이를 연결하는 비용이 주어졌을 때, 1과 0의 비용이 주어지지 않습니다.
- 모든 섬 사이의 다리 건설 비용이 주어지지 않습니다. 이 경우, 두 섬 사이의 건설이 불가능한 것으로 봅니다.
연결할 수 없는 섬은 주어지지 않습니다.
costs를 그림으로 표현하면 다음과 같으며, 이때 초록색 경로로 연결하는 것이 가장 적은 비용으로 모두를 통행할 수 있도록 만드는 방법입니다.
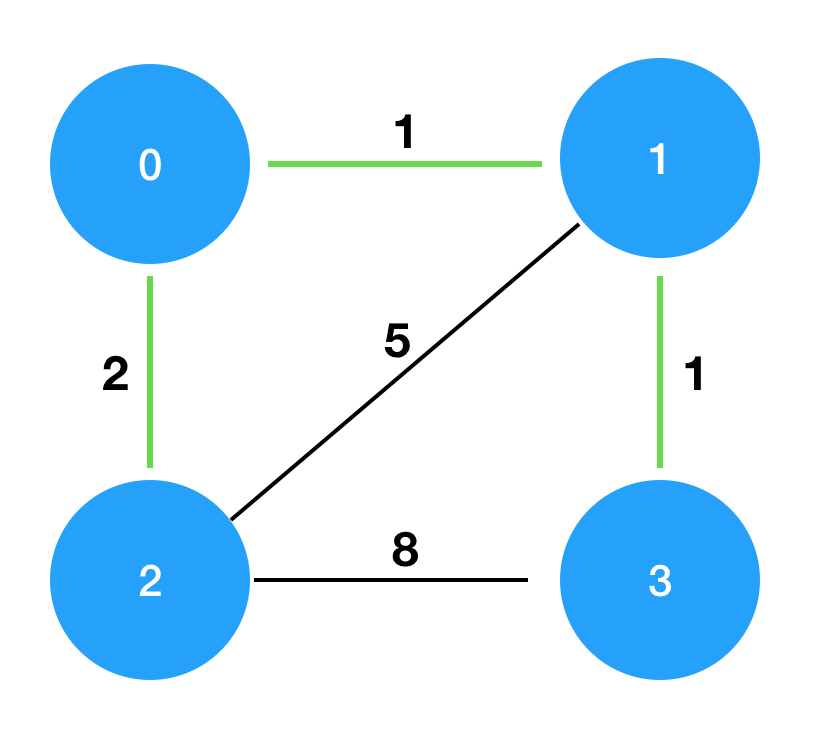
문제풀이
크루스칼 알고리즘을 이용하여 풀어야한다고 한다.
다른사람풀이를 참고하며 풀었다.
크루스칼 알고리즘(Kruskal's Algorithm) 정리
📌 정의
크루스칼 알고리즘은 최소 신장 트리(Minimum Spanning Tree, MST) 를 찾는 알고리즘이다.
즉, 모든 노드를 최소 비용으로 연결하는 트리를 찾는 알고리즘이다.
📌 특징
- 그리디 알고리즘(Greedy Algorithm) 기반 → 항상 가장 작은 비용의 간선을 먼저 선택
- 유니온 파인드(Union-Find) 를 활용하여 사이클을 방지
- 간선 중심 알고리즘 → 간선을 정렬한 후 하나씩 추가
- 시간 복잡도: O(E log E) (E는 간선 개수)
- 간선 정렬 O(E log E)
- 유니온 파인드(합치기 & 찾기) O(α(N)) (거의 상수 시간)
📌 크루스칼 알고리즘 동작 과정
1️⃣ 모든 간선을 비용 기준으로 오름차순 정렬
2️⃣ 가장 작은 비용의 간선부터 선택
- 단, 사이클이 발생하면 선택하지 않음
- 사이클 여부는 유니온 파인드(Union-Find) 알고리즘으로 판별
3️⃣ (N-1)개의 간선이 선택되면 종료 - (N: 노드 개수)
📌 예제 문제
문제
아래 그래프에서 최소 신장 트리를 구하라.
노드 개수: 4
간선 정보 (노드1, 노드2, 비용):
(0,1,1), (0,2,2), (1,2,5), (1,3,1), (2,3,8)
📌 크루스칼 알고리즘 vs 프림 알고리즘
알고리즘 방식 시간 복잡도 특징| 크루스칼(Kruskal) | 간선을 정렬 후 선택 | O(E log E) | 간선 개수가 적을 때 유리 |
| 프림(Prim) | 정점 중심 | O(E log V) | 그래프가 밀집(간선 많음)할 때 유리 |
📌 크루스칼 알고리즘 핵심 요약
✅ "간선을 정렬하고, 가장 작은 비용부터 하나씩 선택"
✅ "사이클이 발생하지 않는 경우에만 추가"
✅ "유니온 파인드로 연결된 집합 관리"
✅ "N-1개의 간선이 선택되면 종료"
📌 실제 적용 사례
- 도로 네트워크 최소 비용 설계
- 전기/통신망 최소 비용 연결
- 컴퓨터 네트워크 설계
유니온 파인드(Union-Find) 정리
📌 정의
유니온 파인드는 서로소 집합(Disjoint Set)을 표현하는 자료구조로,
각 원소가 어떤 그룹(집합)에 속해 있는지를 관리하는 알고리즘이다.
📌 사용 목적
- 특정 노드가 어떤 집합에 속해 있는지 찾기
- 두 개의 집합을 합치기 (Union)
- 사이클 판별(그래프 알고리즘에서 필수)
- 크루스칼 알고리즘에서 최소 신장 트리(MST) 구성 시 사용
📌 시간 복잡도
- 기본적으로 O(N) (트리 깊이에 따라 성능 저하 가능)
- 하지만 경로 압축(Path Compression) & 랭크 기반 합치기(Union by Rank) 를 사용하면
거의 O(1)에 가깝게 동작
📌 유니온 파인드 핵심 연산
1️⃣ Find(찾기):
- 주어진 원소가 속한 집합(부모 노드)을 찾음
- 경로 압축(Path Compression) 기법을 사용하면 트리 깊이를 줄일 수 있음
2️⃣ Union(합치기):
- 두 원소가 속한 집합을 하나로 합침
- 랭크 기반 합치기(Union by Rank) 를 사용하면 트리 균형을 유지하여 성능 개선 가능
📌 유니온 파인드 핵심 요약
✅ "Find: 부모 노드를 찾는 연산 (경로 압축 적용)"
✅ "Union: 두 집합을 합치는 연산 (랭크 기반 합치기 적용)"
✅ "경로 압축으로 트리 깊이를 최소화하여 최적화"
✅ "사이클 판별, MST(크루스칼 알고리즘) 등에서 사용됨"
📌 유니온 파인드 활용 예시
1️⃣ 사이클 판별 (그래프에서 사이클이 있는지 확인)
2️⃣ 크루스칼 알고리즘 (최소 신장 트리, MST)
3️⃣ 네트워크 연결 (같은 그룹에 속하는지 확인)
4️⃣ 집합 찾기 (ex. 친구 관계, 유사 그룹 분류)
비용을 기준으로 오름차순
=> 최소의 비용이 들어야하기 때문에 가장 작은 것부터 선택
bridges => 연결된 부모 섬 (맨 처음
room => 2차원 배열로 부모섬에 연결된 모든 섬 번호 저장
초기에는 섬들이 연결되어 있지 않기 때문에 각 섬의 대표 섬은 자신이고, 자신밖에 존재하지 않는다.
대표섬이 같다면 연결되어 있는중.
나의코드
def solution(n, costs):
answer = 0 #건설비용
made=0 # 만들어진 다리 개수
costs.sort(key=lambda x: x[2]) # 건설 비용 기분으로 오름차순
bridges=[i for i in range(n)] # 연결된 섬 (parents)
room =[[i] for i in range(n)] # 섬에 연결된 섬들
for x,y,cost in costs:
x=bridges[x]
y=bridges[y]
if x==y: continue # 같은 그룹에 속함 # 다른 그룹에 속하면 연결(밑에 코드 수행)
# y 섬에 있는 섬들을 모두 x 섬으로 옮김
while room[y]:
k=room[y].pop()
room[x].append(k)
bridges[k]=x
answer+=cost
made += 1
if made == n-1: # 섬끼리 전부 연결되는 최소 다리 갯수
break
return answer
참고하기
def find(parent, x):
"""경로 압축을 이용한 find 함수"""
if parent[x] != x:
parent[x] = find(parent, parent[x]) # 루트 노드 찾기 및 경로 압축
return parent[x]
def union(parent, rank, a, b):
"""유니온 함수: 두 집합을 합침 (랭크 기준)"""
root_a = find(parent, a)
root_b = find(parent, b)
if root_a != root_b:
if rank[root_a] > rank[root_b]:
parent[root_b] = root_a
elif rank[root_a] < rank[root_b]:
parent[root_a] = root_b
else:
parent[root_b] = root_a
rank[root_a] += 1 # 랭크 증가
def solution(n, costs):
"""
크루스칼 알고리즘을 이용해 최소 비용으로 모든 섬을 연결하는 함수
:param n: 섬의 개수
:param costs: [섬1, 섬2, 비용] 리스트
:return: 최소 비용
"""
costs.sort(key=lambda x: x[2]) # 비용 기준 오름차순 정렬
parent = [i for i in range(n)] # 부모 테이블 초기화
rank = [0] * n # 랭크 초기화
mst_weight = 0
edge_count = 0
for u, v, weight in costs:
if find(parent, u) != find(parent, v): # 사이클이 생기지 않는 경우에만 연결
union(parent, rank, u, v)
mst_weight += weight
edge_count += 1
if edge_count == n - 1: # n개의 섬을 연결하려면 n-1개의 다리가 필요
break
return mst_weight
'프로그래머스 > LV.3' 카테고리의 다른 글
| [프로그래머스][LV.3] 단어 변환 | python3 (0) | 2025.03.22 |
|---|---|
| [프로그래머스][LV.3] 네트워크 | python3 (0) | 2025.03.21 |
| [프로그래머스][LV.3] 아이템 줍기 | python3 (0) | 2025.03.19 |
| [프로그래머스][LV.3] 이중우선순위큐 | python3 (0) | 2025.03.14 |
| [프로그래머스][LV.3] 디스크 컨트롤러 | python3 (0) | 2025.03.13 |