2024. 4. 21. 15:01ㆍ메타코드/머신러닝

이번 시간에는 머신러닝을 배울때 필요한 수학개녕을 배운다.
1강 회귀 :: Basic Math for ML
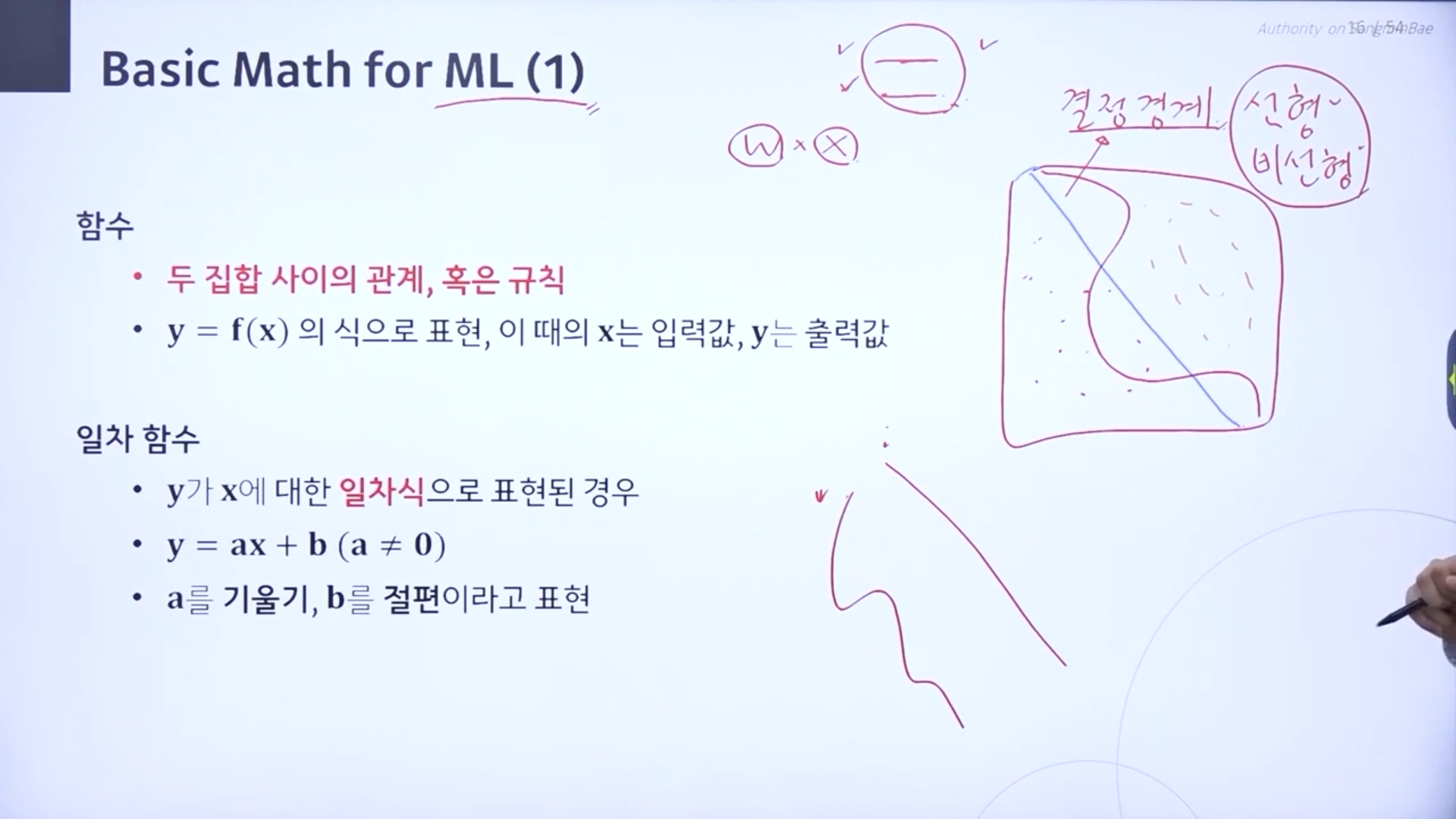
♣결정경계
경계를 나누는 선이 선형이냐 비선형이냐를 본다. 결정경계가 일직선이면 선형이고 꾸불꾸불한 비선형이다.
이것은 회귀모델의 선형 모델,비션형 모델의 선형, 비선형과는 다르다. 회귀모델의 선형,비선형은 모양이라기모다는 데이터와 파라미터 사이가 선형적인 사이로 결합이 되어있냐 아니냐를 말한다.

♣ 함수.
두 집합 사이의 관계, 혹은 규칙을 찾아주는, 맵핑해주는 것을 말한다.
입력되는값을 x로 축력값을 y로 표현한다. 함수는 function의 f로 표현한다.
피처 부분과 라벨을 표현하는 완벽한 관계가 존재할 것이다. 그러한 상황을 표현하기 위해서 y=f(x)로 표현.
♣ 일차함수
y가 x의 일차식으로 표현된 경우
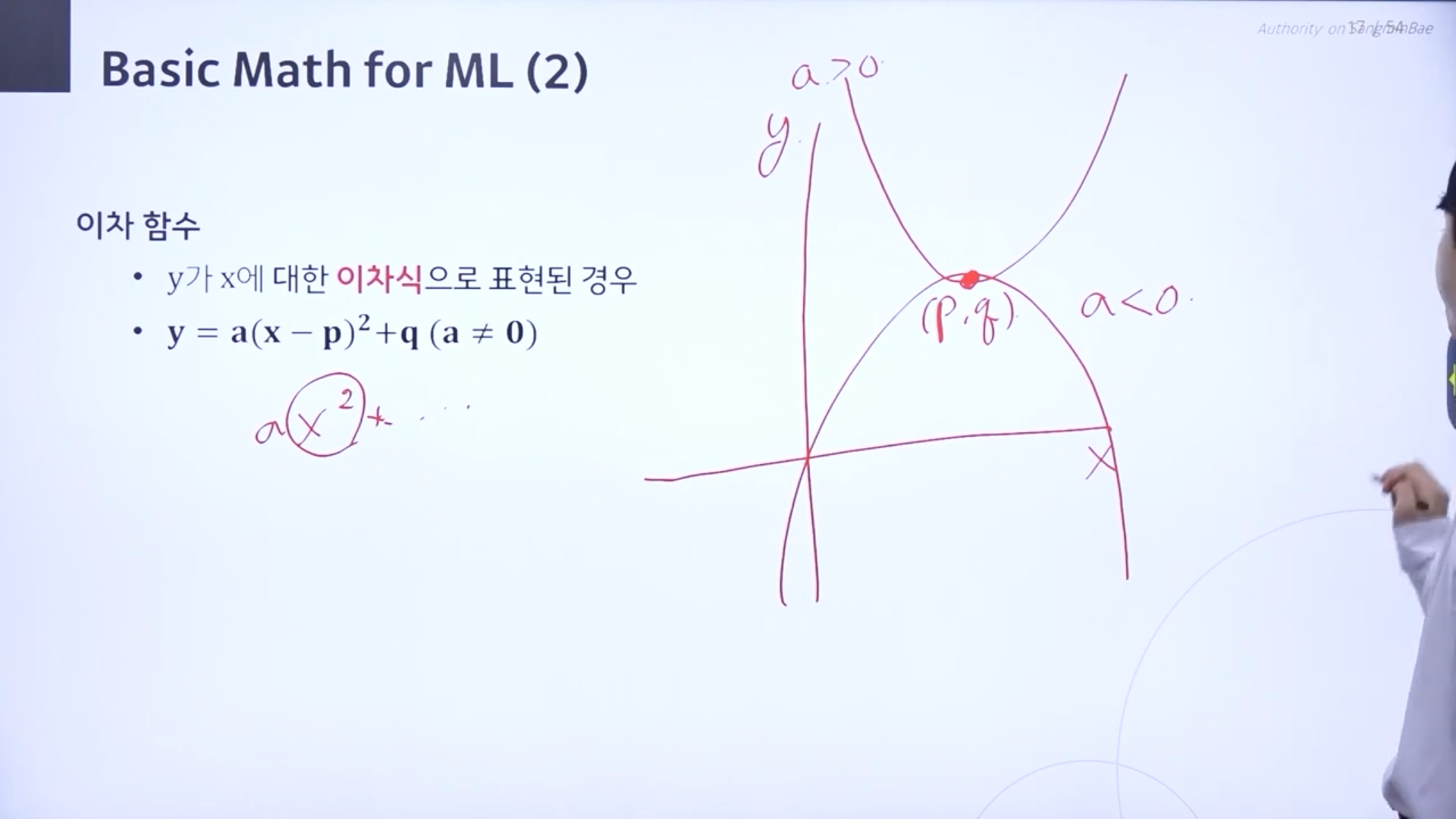
♣ 이차함수
y가 x에 대한 이차식으로 표현된 경우
(p,q)라는 점이 꼭지점이 되는 이차함수
a>0면 아래로 볼록. a<0이면 위로 볼록
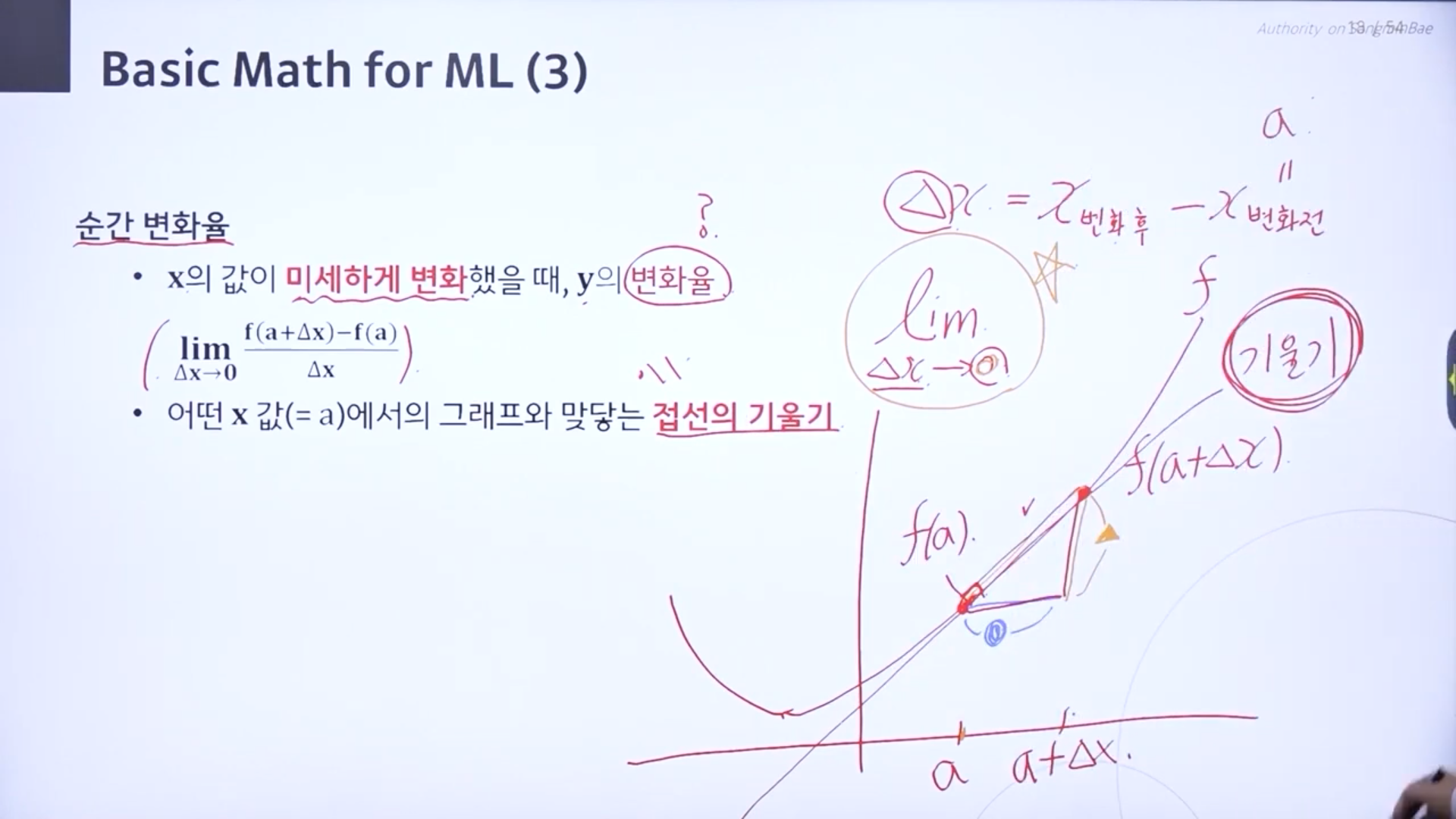
♣ 순간변화율 => 미분
순간변화율은 x값이 순간적으로 변화할때 y의 변화율을 말한다.
델타x = (x의 변화후 - x의 변화전)
델타x의 값이 0으로 무한정 갔을때 어떻게 되느냐가 순간변화율 정의이다.
순간변화율은 접선의 기울기이다.


♣ 미분
함수를 미분한다는 것은 함수의 순간 변화율을 구한다는 뜻이다.
f(x)를 x라는 값에 대해 미분한다.
미분을 하면 한 차수가 낮아진다.
어떤 포인트에서의 순간변화율을 살펴봐서 출력값이 얼마나 바뀌는지 알아보는 과정이다.
♣ 함수의 최솟값
*머신러닝에서 미분이 필요한 이유
함수의 최솟값에서의 미분값은 항상 0이다. 이를 바탕으로 파라미터의 최적값을 구할 수 있다.
실제값 y와 예측값y의 차이(손실값)을 줄여주는(최소화)시켜주는 f헷을 찾는 것이 목표이기 때문에.
손실함수= (y-y헷)의 제곱
순간변화율이 0이 되는 부분이 손실함수의 최솟값이 되는 부분이고, 모델 파라미터를 잘 표현하는 모델의 최적값이라는 것을 알 수 있다. 모델이 학습하고 싶은 위치이다.

♣ 지수함수
x값이 지수인 함수
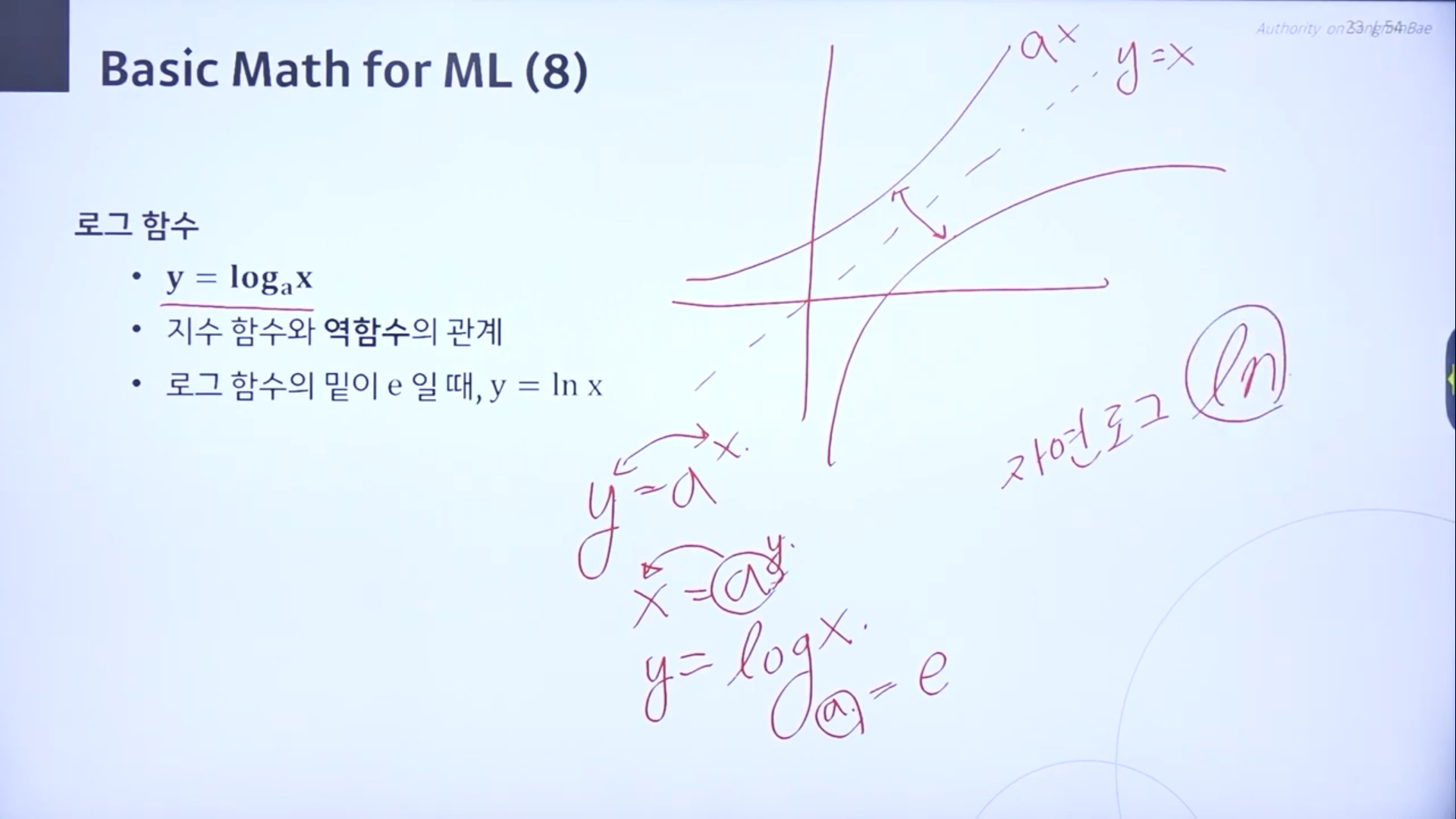
♣ 로그함수
지수함수와 역함수의 관게
로그함수의 밑이 e일때 y=lnx
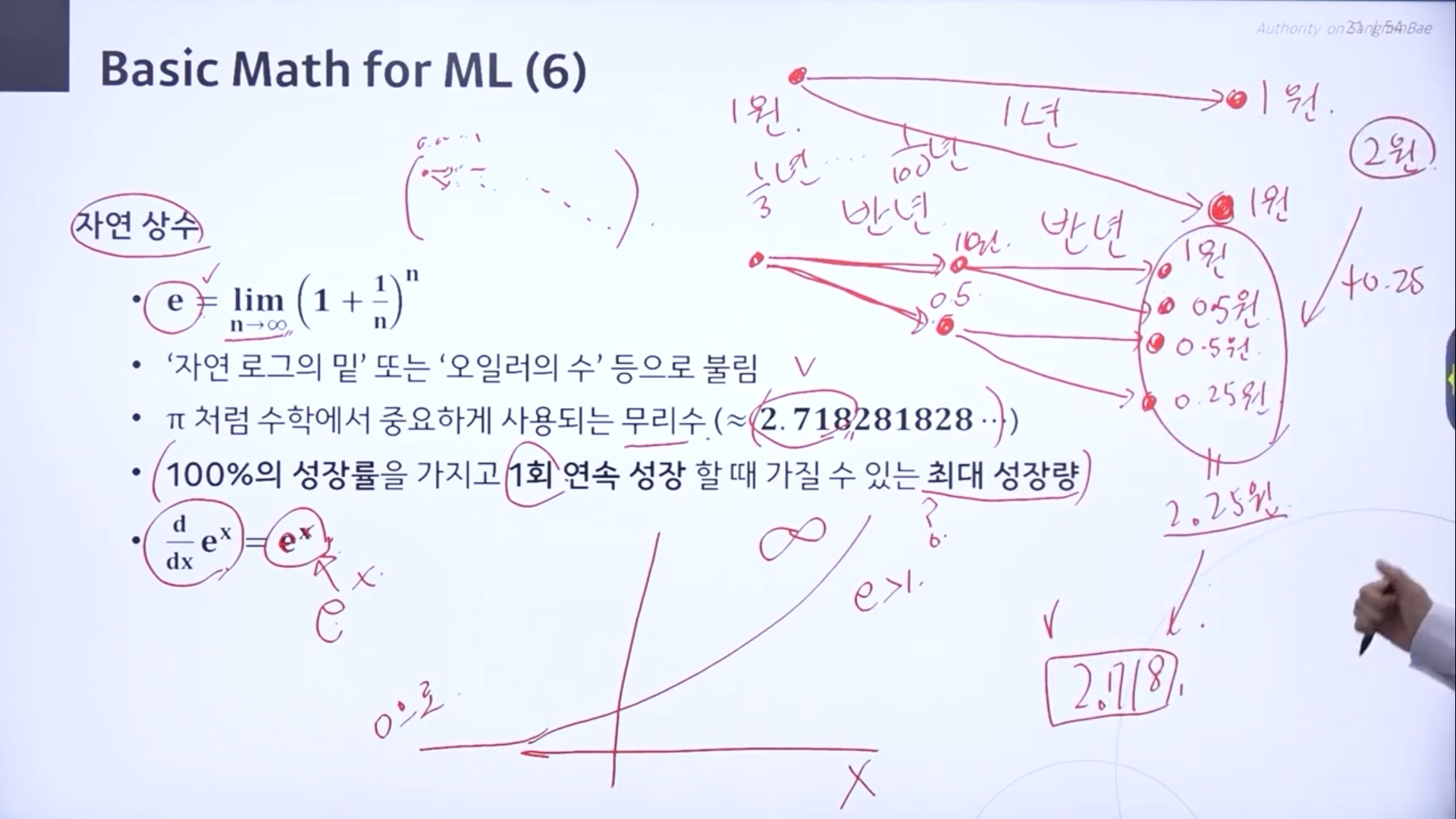
♣ 자연상수
원주율이나 e는 무리수이다.
100%의 성장률을 가지고 1회 연속 성장 할 때 가질 수 있는 최대 성장량
->1원을 가지고 있을때 1년뒤에 100%로 성장시켜서 준다.1년후엔 1원+1원=2원. 이걸 1년이 아니라 반년씩 쪼갤 수 있도록 기회를 줄 때, 반년 후에는 1원 + 0.5원. 다시 반년후에는 1원+0.5원+0.5원+0.25원=2.25. 그냥 1년을 기다렸을때와 값이 다르며 더 늘었다. 이 쪼개는 것을 무한으로 늘릴 때 2.718이 된다.
이걸 자연상수라고 부르고 e로 표현한다. e=2.718...
지수함수에서 밑이 자연상수인 함수는 미분을 취했을때 자기 자신이 된다


자연함수는 시그모이드 함수, 소프트맥스 함수로 연결이 된다.
시그모이드 함수의 출력값은 0보다 크고 1보다 작은 값을 가지게 된다. 중앙값은 0.5이기 때문에 분류문제에 쓰인다.
-> 0.5보다 크면 클래스1로 , 작으면 클래스0으로
각 클래스에 대한 예측값을 확률의 형태로 만들어 줄 때 소프트맥스를 사용한다. 확률은 0~1 사이의 값을 갖는다.
수학쪽은 더 추가 공부가 필요할 것 같다. 시그모이드함수와 소프트맥스 함수도 복습을 해야 겠다.
'메타코드 > 머신러닝' 카테고리의 다른 글
| [머신러닝] 머신러닝 입문 올인원 :: 1강 회귀_Gradient Descent (0) | 2024.05.30 |
|---|---|
| [머신러닝] 머신러닝 입문 올인원 :: 1강 회귀_Least square method (0) | 2024.05.05 |
| [머신러닝] 머신러닝 입문 올인원 :: 1강 회귀_Linear Regression (1) | 2024.05.05 |
| [머신러닝] 머신러닝 입문 올인원 :: 1강 회귀_Notation (0) | 2024.04.21 |
| [머신러닝] 머신러닝 입문 올인원 :: 1강 회귀_인사/강좌소개 (0) | 2024.04.21 |
